4x4x4・解法の分類と考察
4x4x4の解法は多岐にわたりますが、現在スピード向けの解法として広く使われているものは数が限られています。
とはいえ現在主流の解法の機構はなかなかに複雑であり、そのシステムやメリットを理解するにあたって、解法の発展の流れを知っておくことは大きな助けとなります。
このページでは、4x4x4のスピード向け解法の分類、発展の流れ及び解法の特徴やメリットに関する考察を行っています。
※筆者による独自の考察、独自の用語定義が含まれます。また、時系列的な歴史に関する考察は行っていません。
解法の分類
まずは今回取り扱う解法を分類しておきます。こちらの図をご覧ください。
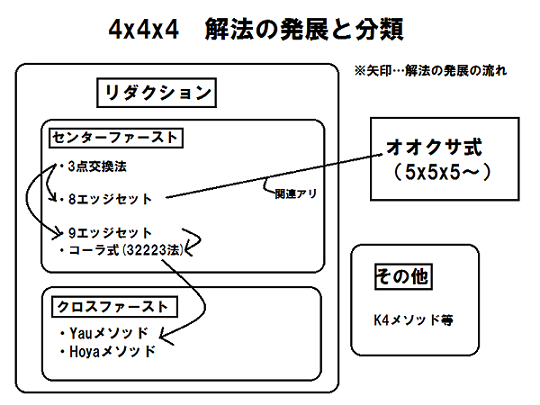
まず最も大きな分類として、「リダクションであるか否か」という点があります。リダクションとは、一度3x3x3の状態にして揃える解法全般のことを指します。これは3x3x3の状態にしさえすればいいため解法の自由度が高く、それゆえスピード競技に適した解法となっています。また、3x3x3の解法を知っている人なら習得が容易というメリットもあります。
その他の解法も多くありますが、スピードに適した解法はほとんどありませんので、今回リダクション以外は詳しく説明しません。K4メソッドに関して詳しく知りたい方はこちらへどうぞ。
続いてリダクションの分類として、どこを最初に揃えるかという分類があります。大きく「センターファースト」「クロスファースト」に分けられます。他にも「エッジファースト」などがありますが、スピード向けではないため今回は割愛します。
センターファーストは最初にセンターを揃える解法です。3点交換法、8エッジセット、9エッジセット、コーラ式などが該当します。
クロスファーストは最初に3x3x3のクロスを完成させる解法です。Yauメソッド、Hoyaメソッドなどが該当します。
今回はこれらの6つの解法について考察していきます。
解法の解説
後述の「解法の考察」でより詳しく説明しますので、簡単な説明にとどめておきます。
・3点交換法
センターを揃えた後、エッジを3点交換をひたすら用いることによって揃えていく、最も初歩的な解法です。
・8エッジセット法
いわゆる5x5x5以上における「オオクサ式」と同等のものです。
中段の1層をずらし続けることによって最後の4つまでを素早く揃える解法です。残り4つ以降は3点交換法と同じです。
・9エッジセット法
中段をずらすことにより、最大で3個のエッジを同時に揃えることができます。
この「ずらし」を3回用いることにより、最大で3x3=9個のエッジを素早く揃えられるという解法です。それ以降は3点交換法と同じです。
・コーラ式(32223法)
中段の「ずらし」を1度だけ利用してまず3個のエッジを揃え、残りはこのエッジの揃った中段を使用し、3点交換法と同様にして2つずつエッジを揃えていく解法です。センターファースト解法としては最も早いとされる解法です。詳しくはこちらへどうぞ。
・Yauメソッド
先にクロスを完成させてからエッジを揃えることにより、さまざまなメリットを生み出している解法です。クロス以降の揃え方はコーラ式と同じです。詳しくはこちらへどうぞ。
・Hoyaメソッド
Yauメソッドとはクロスを揃える順序や手法が若干異なる解法です。クロス以降はYauメソッドと同じくコーラ式に従います。詳しくはこちらへどうぞ。
解法の発展
まず、最も基本的と考えられるのが3点交換法です。
3点交換とは、こちらのような手順を使うことでエッジのうち3つを交換し、エッジを揃えていくことです。

u' R U' R' Uw
(画像は正面がF面)
3点交換は3つのステップからできています。
①中列をずらして1つのエッジをペアリングする
②揃ったエッジをずらした中列から出し、関係ないエッジを入れる
③ずらした中列を戻す(②で入れるエッジを工夫すると、ここでもう1つエッジを揃えることができる)
という感じです。
リダクションにおけるエッジペアリングは、この3点交換が最も基本的な形です。
どのような解法であろうと、中段をずらすことでエッジをペアリングしていくというのは変わりません(当たり前っちゃ当たり前ですが)。
最後に2点交換を使うこともありますが、これも基本は同じです。
①中列をずらす
②エッジを反転させる
③ずらした中列を戻す
という流れになっています。
閑話休題、3点交換法というのは、センターを揃えた後にこの3点交換だけを用いることでエッジを揃えていく解法です。
ただこれでは一回一回中列を戻さなければならず、また正しいエッジを探すのも大変で、非常に時間がかかってしまいます。
これを解消するために、これ以降の解法では様々な工夫が凝らされています。
まず、中段を戻すのが面倒であれば中段を戻さずに揃えていって最後に戻せばいいのではないか?という考えの元生み出されたのが8エッジセット法です。
センターを揃えたあと1つの中列をずらしたままにしておきます。この中列を使い続ければ、中列を戻す手間がなくなります。これにより時間を短縮することができます。
ただし、最終的には中列を戻さなければなりません。また中列には4つのエッジが挟まっているので、上の方法で揃えることができるのは8つまでです。これが8エッジセット法の名前の由来です。
ただこれは上記のように短縮できるのが中列を戻す部分だけであり、またずらす中列が固定になるため制限が多く、あまりメリットは大きくありません。この解法が威力を発揮するのは5x5x5以上の多分割においてです。
多分割はパーツ数が増えるため、後に書くようなギミックを凝らした解法は使用が難しくなります。そのため、5x5x5以上の多分割においてはこの解法が主流になっています。
余談ながら、5x5x5以上ではこの解法はオオクサ式と呼ばれています。これは日本の大艸(おおくさ)さんという方が5x5x5で使用していたことから名前がついています。
また、これとは別の短縮方法も考え出されました。
一回中列をずらすと、4つのエッジが交換されます。3点交換法ではこれが厄介となってくるのですが、逆にこれを利用すれば一度の中列をずらす動きでもっと沢山のエッジを揃えられるのではないか?と考える事により生み出されたのが9エッジセット法です。
中列をずらすとライン上にある4つのエッジが同時にずれるわけですから、一つだけでなく他のエッジも揃うようにエッジを組んでおけば、同時に複数のエッジを揃えることが可能です。
考えられる最大値は4つですが、実際は4つ同時に揃えられるようになっているのは稀で、3つが同時に揃えられます。以下、これを「ずらし」と呼ぶことにします。
この「ずらし」を3回使えば、エッジを3x3=9個程度揃える事ができます(実際の数は多少前後します)。残りエッジが4つより少なくなると「ずらし」は使えないため、この解法で揃えられるのは9個程度です。これが9エッジセットの名前の由来です。
この解法の弱点は、持ち替えが多いのでパーツを認識するのが少し大変であることと、途中でペアリングが切れてしまった場合の対応が面倒であることです。
例えばエッジが2パーツの交換になっていた場合は、「ずらし」による揃え方はできません。こうなると途中で別のパーツを挟んだりすることになるので効率が悪くなります。
9エッジセットでは「ずらし」を必ず3回行うので、こういうアンラッキーが高い確率で起こってしまいます。
この点を改良して生まれたのがコーラ式(32223式)です。
コーラ式はいわば9エッジセットと3点交換法のハイブリッドの解法で、センターファーストでは最も速いです。
詳しくはこちらを見て下さい。
まず、1回だけ「ずらし」を行うことで3つのエッジが揃います。最初の1回だけですので、9エッジセットと違ってうまくいかないケースは稀です。
そして、この「ずらし」を行った段と2つのスロットを使い、3点交換を行って2つずつエッジを揃えていきます。
この解法でのメリットは、
・9エッジセット法で起こりがちなアンラッキーがほぼ発生せずもし発生しても効率を落とさずに処理できること
・3点交換と違ってずらす中段が固定になり、また中段奥のエッジが必ず埋まっているため、目的のエッジを探しやすくなること
などです。デメリットもほぼ0です。
このように非常に優秀な解法のため、少し前まではトップキュービストの間でもほとんどの人がこちらの解法を使用していました。
ところで、コーラ式や8エッジセット、9エッジセットにおいてはエッジペアリングに用いる中段は常に一定で、上下8つのエッジは基本的に解法に影響しません。また、上下のエッジはステップが進むにつれどんどん埋まっていきます。
センターファーストだとどこが埋まっていくかというのは場合によってまちまちなのですが、特定の場所、さらに言えば3x3パートのクロスの部分を先に埋めてしまうように決めておけばいろいろとメリットが生まれるのではないか、という発想のもと生まれたのがクロスファーストです。
クロスファーストの解法では、センターを全て揃える前にクロスエッジをある程度揃えてしまいます。これにより、エッジを始める際に既にクロスが完成しているような形になり、エッジは残り8個を揃えればよいという形になります。
最後のエッジ8つは、3点交換方法や8エッジセットなどではあまり効率良く揃えることはできませんが、コーラ式を用いるれば非常に効率よく揃えることができます。コーラ式が開発されたことも、クロスファーストの発展に大きな役目を果たしていると言えます。
クロスファーストは、センターファーストと比較して
・クロスエッジパートにおいてセンターの制約が少ないため自由度が高く、上手くやれば手数の短縮になる
・エッジパートでD面を見る必要がないため判断効率が段違いに良い
・3x3パートをF2Lから始めることができるため手数、判断効率ともに良い
などのメリットがあります。特に3つ目の点ですが、多くの人はクロスを素早く読むのは慣れていないのに対しF2Lを素早く読むのには慣れている場合が多いため、手数だけでなく判断効率においても非常に優位であるといえます。
逆にクロスファーストにおけるデメリットは、
・クロスエッジパートにおいてセンターの制約が少ないため自由度が上がり、判断が難しくなる
・センターパートにおいてセンターを揃える順番やクロスエッジによる制約があるため、多少手数が増える
・3x3パートの解法がほぼCFOPのみに制限される(Rouxなどでは有利にならない)
・全体として工程が多く複雑になるため、習得に時間を要する
などがあります。
総合して見た場合、現在はクロスファーストの方がスピードの上でメリットが多いとされ、トップキューバーのほとんどがクロスファーストを採用しています。ただこれはあくまで「現在は」ということであり、かつてはデメリットの方が強いと考えられていましたし、今後それがまた覆る可能性も無いとはいえないということです。
このあたりの考え方の変遷をみるのも、キューブの歴史を考える上で興味深い点であるといえます。
クロスファースト解法の比較
クロスファースト解法であるYau MethodとHoya Methodを比較してみましょう。
詳しい解法の説明は省きます。
Yau MethodとHoya Method、それぞれの特徴は以下のような感じです。
Yau Method
・最初に揃えるセンターの選択肢が2面のみ(クロス面かその対面)
・クロスエッジパートでの自由度が高く手数を短くできるが、その分複雑で考える事が多い
・センターパートでの制限が多少強いが工夫すればさほどデメリットにはならない
・全体として工程がやや複雑
Hoya Method
・最初に揃えるセンターの選択肢が4面(クロス面とその対面以外)
・クロスエッジパートはパターン化が可能なため考える事は少ないが、手数が多くなりがち
・センターパートでの制限がほぼないので素早く出来るが、センターはそもそもソルブでの時間的割合が少ないためあまりメリットにならない
・全体として工程がやや単純
総合的に見て、Hoyaは比較的わかりやすい代わりに手数の多い解法、Yauは手数が少ない代わりに複雑な解法だと言うことができます。
現在の世界トップにおける解法のシェアから考えるに、現時点ではYauの方がスピード面では優っていると言えるでしょう。
ただ、解法の習得の容易さなど多面的に考えた場合、どちらが優れているとは一概には言えません。
おわりに
現在のスピードキューブにおける解法は、昔と比べるととても複雑で、またさまざまな考え方やテクニックを用いています。最近キューブを始めたという人は当たり前のように感じていること、また逆に「なんでこんな発想ができるんだろう」と思うようなことも、キューブの歴史のなかで様々な人が様々なことを考えて、その結果として今存在しているということです。そのことを知っていれば、解法の考え方やその妥当性を理解することにもつながるでしょう。
そして、スピードキューブの世界に終わりはありません。解法もまだまだ発展の余地があります。そしてその発展は、これまでの発展の延長線上にあるはずです。
スピードキューブの歴史、考え方の変遷を学び、また自分で様々なことを考えることで、新たな知見が生まれてくることもあると思います。新たな解法、新たな歴史を生み出すのは、あなたかもしれません。
(2014年5月15日 執筆:HATAMURA)